Exposure Time Calculator description¶
The following description of the Exposure Time Calculator (ETC) provides details to those who are interested. One does not need to read and understand this in order to use the ETC and plan a survey.
A detailed description of various properties of the ETC can be found in the ETC Requirements Specification [VIS-SPE-4MOST-47110-1740-0001].
The ETC is supposed to provide the user with some idea of how long the exposure times would be on average for a given target. The 4MOST instrument is simulated by the Top Of the Atmosphere to Detector (TOAD) instrument simulation software, which accounts for numerous instrumental, environmental, and material effects. While there are many physical effects that introduce variations in the sensitivity of 4MOST between fibres and over time, the ETC can only present one average value of the throughput. This is because, due to the survey nature of 4MOST programs, the user will not be able to choose sky conditions for their observations. The only choice that is offered is dark/grey/bright/superbright sky.
The ETC therefore uses time-average and fibre-average properties, which do not correspond to a “real” observing condition and instrumental setup. For example, the ETC uses an average fibre transmission curve, a fibre average area of \(\langle A_{fibre} \rangle = 1.605\) arcsec² with the average radius, \(\langle r_{fibre} \rangle = 0.71476\)”, and assumes that the fibre is in the center of the field. Such a fibre does not exist – the real central fibre does not have this area and this transmission curve.
ETC characteristic data¶
For a point source, the following telescope and instrumental effects are considered. For extended sources, the transmission curves account for the same effects, but ignore vignetting on the fibre core, and hence the input light is scaled with the fibre pupil internally by the ETC. The profiles of extended sources are convolved with the seeing disk.
Atmospheric extinction¶
The atmospheric extinction is a complex function of airmass, cloud cover, temperature, density, chemical composition and wavelength.
The ETC uses data from ESO SkyCalc for computing the wavelength dependent extinction as a function of airmass for standard environmental conditions.
Sky brightness¶
The sky brightness is a function of zodiacal light, sky emission lines, airglow and moon brightness. Zodiacal light is a function of pointing and time of year, emission lines are a function of air chemistry, airglow is a function of zenith distance and the moon brightness is a function of moon phase, moon height over horizon, target distance to the moon and the airmass of the target.
The ETC uses four fixed values of year-averages for dark, grey, bright, and superbright time. It is using parameterized data from SkyCalc to estimate sky brightness.
Seeing¶
At Paranal, the seeing FWHM ranges between 0.3” and more than 3” at zenith. The seeing is closely modelled by a Moffat distribution with β=2.5. The latest seeing statistics on Paranal are:
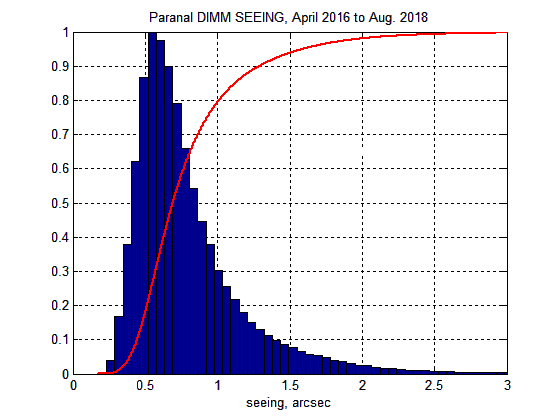
The ETC uses a fixed median seeing of 0.8”, based on old statistics of DIMM recordings between June 2014 and September 2017. The new statistics from April 2016 to August 2018 show an improved median seeing of ~0.7”, however, these data were unavailable when the decision on what value to use was finalized. The ETC therefore uses a slightly pessimistic seeing value, giving a conservative estimation on the performance.
Mirror reflectivity¶
Mirror reflectivity is a function of wavelength and a function of time due to dust contamination and cleaning events.
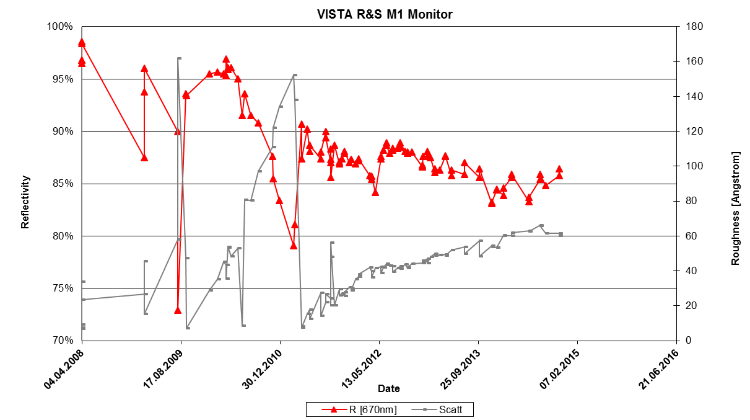
The ETC uses the mirror reflectivity as a function of wavelength at around 86% as it would be just after a mirror cleaning with CO:subscript:`2`. The value is worse than after re- coating but can be expected most of the time during the lifetime of 4MOST.
Telescope vignetting¶
The telescope induces some light loss as a function of field position. This includes a vignetting of 2% due to the angle of illumination of the spider vanes. The undersized M2 also influences the shape of the light cone that is coupled into the fibre. This has knock-on effects on the vignetting in the spectrograph pupil and image properties on the grating.
The ETC only simulates field centre.
Telescope PSF¶
The telescope PSF is a function of the 2D field position, fibre focus, ADC angle position and wavelength. The ADC is rotated depending on the zenith angle, and so the telescope PSF also depends on the zenith angle by proxy of the ADC.
The ETC only uses the telescope PSF at field centre and slightly out of focus when the telescope is pointing at zenith. It simulates the PSF as a function of wavelength.
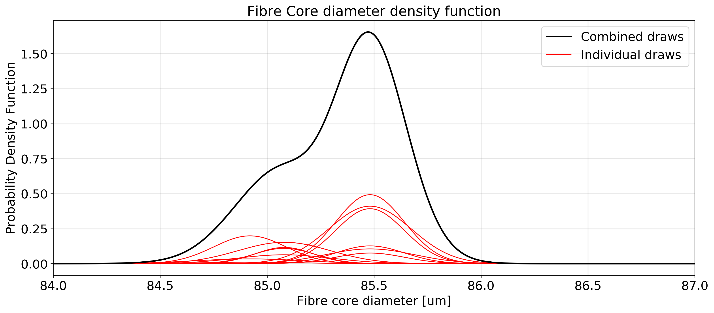
Physical fibre size¶
The physical fibre size is manufacturing dependent according to the statistics below.
The ETC uses a fixed fibre core diameter of 85 µm.
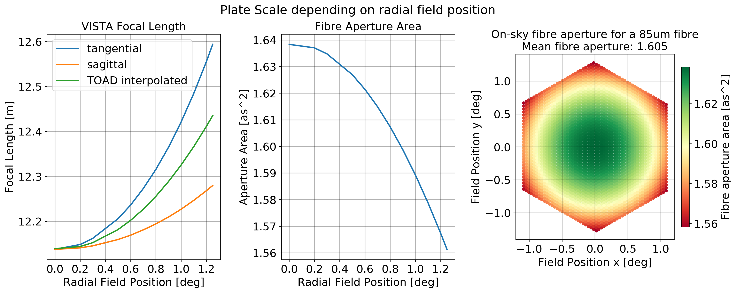
Fibre aperture size¶
The fibre aperture on sky is a function of field position for a fixed fibre core size. The values range between 1.56 arcsec² at the edge of the field and 1.63 arcsec² at field centre for a 85 µm fibre core diameter.
The ETC uses the area mean plate scale over the focal surface. For a 85 µm diameter fibre core this value is 1.605 arcsec².
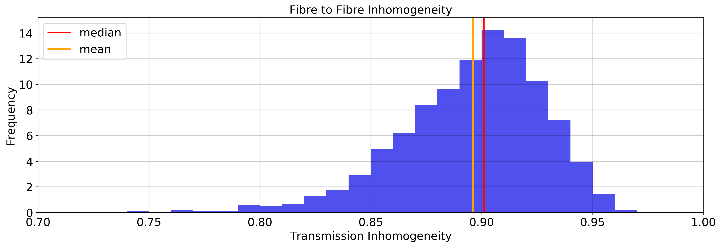
Intrinsic fibre transmission efficiency¶
Each fibre has an intrinsic transmission efficiency that is relatively stable over time and depends on fibre cable manufacturing, specifically the alignment of the fibre in the connector. The expected distribution is presented below.
The ETC uses the mean fibre transmission efficiency of 0.896.
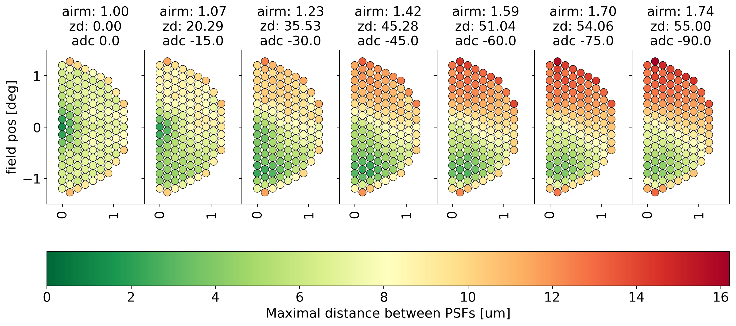
Residual atmospheric dispersion¶
The atmospheric dispersion is a non-linear function of airmass and describes the broadening of a point source as a function of wavelength. The ADC is a linear compensation in wavelength as a function of airmass. The residual ranges between 0 (field centre, zenith) and 0.25” (i.e. 15 µm at field edge, 55° zenith distance).
The ETC does not take the residual atmospheric dispersion into account because it computes transmission efficiency at field centre at zenith, which has no residual atmospheric dispersion.
Fibre to target alignment¶
The fibre to target alignment is a function of positioner accuracy, metrology accuracy and astrometric solution. We expect an RMS error of less than 0.2” based on error budgeting. For a normal distribution, 67% of all cases would be smaller than 0.2”. The actual distribution will be measured at commissioning.
The ETC uses a fixed offset between fibre centre and target position of 0.1”.
Fibre Focal Ratio Degradation¶
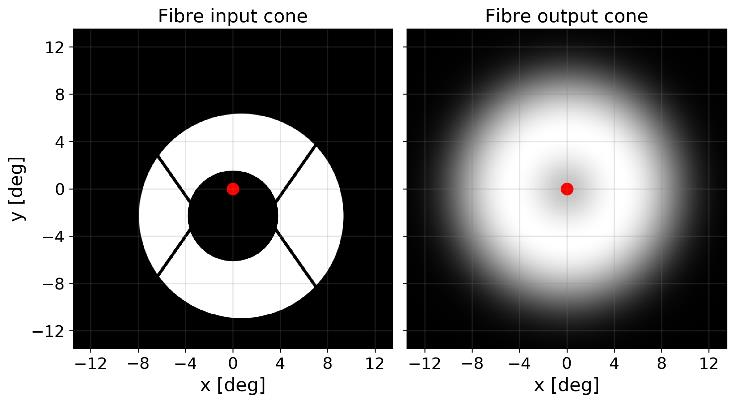
Focal Ratio Degradation (FRD) is an effect that describes how the shape of the light cone which is coupled into the fibre is changed at its output. The cone always becomes larger, but the exact properties are not stable. The broadening is a function of fibre manufacturing quality, stress on the fibre as well as fibre routing. The FRD characteristics of each fibre are unique. And because the telescope cable wrap moves the fibre over time, the effect is not stable.
The ETC uses one fibre FRD model, that is based on lab measurements but is constant for all simulations.
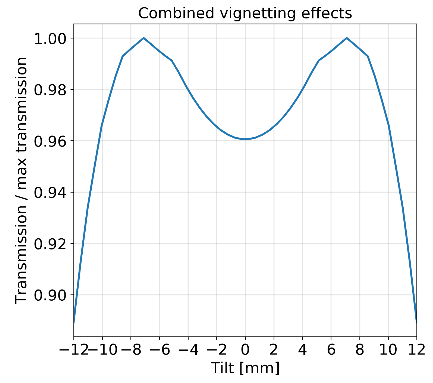
Fibre tilt induced vignetting losses¶
The fibre tilt introduces two effects. At the fibre entrance, the tilt causes a focus shift, which influences the telescope PSF as seen by the fibre. At the fibre output, the tilt induces a broadening of the light beam, which is vignetted by the spectrograph optics. See below for a transmission loss as a function of tilt.
Uniform extended sources only experience tilt-induced broadening at the fibre output, because then the telescope PSF is irrelevant. In that case the corresponding transmission vs. tilt profile does not have a dip in the centre because the latter is caused by the defocus at the fibre input.
The ETC simulates transmission efficiency only for non-tilted fibres, which have the minimum losses in the spectrograph but non-optimal properties due to the focus position
Detector characteristics¶
The detectors have 4 quadrants with 4 individual read out noise values, dark current values and gain values.
The ETC uses the mean of all quadrants in one detector for all 3 parameters. For LRS, the average value of LRS-A and LRS-B is used.
Detector transfer efficiency¶
The detector readouts are at the detector corners. Therefore, the charges from the detector centre travel through more pixels during readout, which induces more loss at the centre than at the edges of the detector of about 1%. Since fibre images are distributed over the entire surface, the transmission loss is a function of slit position.
The ETC uses a fibre close to the centre of the slit.
Spectrograph image quality¶
The image quality of the spectrographs is a function of slit position, and wavelength. The slit position dependency is further subdivided as a function of global slit position and local position in a slitlet. This is because the slitlets approximate the ideal slit shape in linear segments. Each slit is populated with 28 slitlets and 29 fibres in each slitlet.
The ETC only simulates the image quality for one fibre at the centre of the slitlet next to the centre of the slit (30 slitlets make one slit).
Material transmission efficiency¶
There are many components that influence the transmission efficiency as a function of wavelength but are otherwise static.
The ETCs use the latest measurements on all these components, including: WFC/ADC glass and surfaces, fibre input surface, fibre glass extinction, fibre output surface, spectrograph collimator reflectivity, VPH grating transmission efficiency, dichroic transmission/reflection efficiency, spectrograph camera transmission efficiency and detector quantum efficiency.
Note that the telescope mirror reflectivity is a function of time and listed separately above
ETC sky¶
The ETC applies atmospheric extinction/absorption using ESO SkyCalc spectra. There are three pre-defined sky conditions for bright, grey, and dark sky brightness, which translate into the following values of the fraction of lunar illumination (FLI):
- “dark” time
corresponds to FLI = 0.090 (Sun/Moon sep = 35°)
- “grey” time
corresponds to FLI = 0.500 (Sun/Moon sep = 90°)
- “bright” time
corresponds to FLI = 0.899 (Sun/Moon sep = 143°)
- “superbright” time
corresponds to FLI = 0.998 (Sun/Moon sep = 175°)
The Moon/target separation is fixed to 45° and the Moon altitude to 45° in all three cases. As an example, for an airmass of 1.2, the pre-defined sky conditions have the following surface brightnesses in AB magnitudes per arcsec²:
Filter |
dark |
grey |
bright |
superbright |
|---|---|---|---|---|
B |
22.24 |
20.77 |
19.36 |
18.43 |
V |
21.49 |
20.47 |
19.23 |
18.39 |
R |
21.09 |
20.33 |
19.23 |
18.46 |
Signal to noise calculation¶
The equation below is used to compute the signal-to-noise ratio (SNR) per spectral pixel, where one spectral pixel may consist of multiple detector pixels, depending on the binning factor. Note that on-detector binning of pixels is only possible in the dispersion direction, but not in the cross- dispersion direction.
where \(N_{obj}\) is the detected target object flux (no background) in e-/s, collected over an area of sky corresponding to the fibre aperture and integrated over one pixel in wavelength (consisting of \(n_{bin}\) detector pixels), \(N_{sky}\) is the equivalent background flux in e-/s, \(t_{exp}\) is the total integration time in seconds, \(n_{exp}\) is the number of exposures, \(n_{CD}\) is the number of pixels in the cross-dispersion direction over which the target and sky fluxes are assumed to be spread (taken to be \(n_{CD}\)), \(n_{bin}\) is the on-detector binning factor (possible values: 1, 2, or 4), \(N_{dark}\) is the dark current in e-/pixel/s, and \(N_{ron}\) is the readout noise in e-/pixel/exposure.
The ETC does not fully simulate the spread of the target and background flux across pixels in the cross-dispersion direction. It simply takes into account the dark current and read-out noise contributions from \(n_{CD}\) pixels without computing an explicit spatial extraction. The SNR per Ångstrom of the extracted spectrum may be computed as
where \(N_{pix}\) is the number of spectral pixels in 1 Ångstrom, which varies with wavelength, spectrograph, arm and on-detector binning factor. For example, at 𝜆 = 450 nm in LRS blue, 1 nm = 10 Å = 32 pixels (for 𝑁𝑏𝑖𝑛 = 1). At 𝜆 = 650 in HRS red, 1 𝑛𝑚 = 10Å = 89 pixels. The ETC works with tabulated unbinned pixel width values in nm as a function of wavelength for each spectrograph and arm.
Galactic reddening¶
The ETC applies reddening using the extinction model fitzpatrick99 [1999PASP..111…63F].
Airmass¶
The ETC uses a representative airmass for each object. This is measured from the observability of the object over the course of one year. For targets with declination greater than -79.6°, the ETC assumes the representative airmass corresponds to when the target is ±15° away from the celestial meridian (i.e. 1 h in hour angle). The declination of a target is converted to altitude, and then to airmass via
Where \(\mathrm{HA}\) is the local hour angle (15° at Paranal), \(δ\) is the declination, \(a\) is the altitude, and \(φ\) is the local geographical latitude (-24.623° at Paranal). This assumes a simple parallel plane model for the atmosphere, which is not precise for observations close to the horizon because it neglects the curvature of the earth. It is, however, well suited until about 70° zenith distance. 4MOST is not configured for optimal performance for zenith distances larger than 55°, which is a limitation imposed by the ADC.