Introduction¶
The 4MOST Exposure Time Calculator (ETC) is mainly a simple simulation facility for the preparation of 4MOST observations.
The ETC consists of a Python package qmostetc with several
modules to simulate atmosphere, telescope, spectrograph, etc., which
can be combined, and a simple tool to process a catalog.
The package makes extensive use of astropy.units, so values
are accompanied with units whenever this is useful. Instead of the
units specified in the documentation, equivalent units may be used as
well (i.e. Ångström instead of Nanometers).
Installation¶
The ETC is distributed as a Python package from Gitlab. It requires at least Python 3.8 to run. The recommended method is using pip from the 4MOST public Python repository:
$ QMOST_PYPI=https://gitlab.4most.eu/api/v4/projects/212/packages/pypi/simple
$ pip3 install --extra-index-url $QMOST_PYPI qmostetc
This will install the most recent stable release, including all packages that are required to run. Aside from the Python package, it installs a script Catalogue processing for the processing of catalogue files.
For 4MOST consortium members, the package can be also installed from a local clone of the Gitlab repository. It can also be run directly from that directory:
$ git clone --recurse-submodules git@gitlab.4most.eu:OpSys/etc.git
$ cd etc
Keep in mind that this installs the latest staging version, so expect glitches and report them in Jira.
Running the ETC tool¶
The basic usage is running the Catalogue processing Python script. The script takes either one file, the YML file containing the setup, or five file names with the content. An example YML file would be
catalog: qmostetc/tests/targets.fits
ruleset: qmostetc/tests/rules.csv
rules: qmostetc/tests/rulesets.csv
templates: qmostetc/tests
resultfile: example_result.fits
The resultfile entry is optional. If it is missing, the result
file name is derived from the YML file by replacing the suffix with
.fits. The file names given in the file are relative to the YML
file. Note that the result file will be overwritten without further
warning.
With this YML file, an example run would look like
$ ./tools/process_catalogue -y example.yml
Total 1 entries
Total 1 target/magtype combinations
Total 1 rulesets
Creating 1 chunks with 1024 entries each (24 cores)
.
Total elapsed time 0:00:00.130151 (130.15 ms per entry)
Without the use of an YML file, the same result can be reached with
$ ./tools/process_catalogue -c qmostetc/tests/targets.fits \
-R qmostetc/tests/rulesets.csv -r qmostetc/tests/rules.csv \
-t qmostetc/tests -o example_result.fits
Total 1 entries
Total 1 target/magtype combinations
Total 1 rulesets
Creating 1 chunks with 1024 entries each
.
Total elapsed time 0:00:00.116244 (116.24 ms per entry)
The tool takes advantage of multiple CPUs and hyperthreading and will use parallelization if possible.
Since the execution may take several hours, the input files are tested first for potential problems. If an inconsistency is detected, the tool stops before processing the catalogue.
To debug the calculated exposure time for individual targets, the Debugging individual targets tool can be used. It prints out intermediate values to calculate the SNR for the estimated exposure time.
Estimating exposure times¶
Estimation of exposure times is the main goal of the ETC. The
criterion is formulated as a simple expression, given as a
qmostetc.Ruleset, which combines qmostetc.Rule objects
containing the aggregation of spectral properties within a given
wavelength range.
The simplest way to give a target spectrum is to use
qmostetc.SEDTemplate, which represents a single template from the
list of standard templates, or given as a file name. The template can
be called with the magnitude and filter system to retrieve the
flux. The wavelength is an attribute of the qmostetc.SEDTemplate
object.
Here is an example that takes requires the signal to noise ratio in two wavelength ranges (one in the red, one in the green arm of the LRS) to be both larger that 50 for a Pickles template spectrum:
import numpy as np
import astropy.units as u
from qmostetc import SEDTemplate, QMostObservatory, Ruleset, Rule
# Object to simulate the 4MOST observatory, including atmosphere,
# telescope, spectrograph, CCD.
qmost = QMostObservatory('lrs')
# Rules to check for minimal SNR of 50 in two wavelength ranges
# Note that one needs to specify the spectrograph arm in the rule.
rules = [Rule(qmost['red'],
'snR', 1*u.nm, 750.*u.nm, 770.*u.nm, 'snr', np.mean, 50.),
Rule(qmost['green'],
'snG', 1*u.nm, 590.*u.nm, 610.*u.nm, 'snr', np.mean, 50.)]
# Combine both rules so that both must match ('and')
ruleset = Ruleset('example', 'snG and snR')
ruleset.set_rules(rules)
# The observation with certain conditions: airmass (zenith angle), seeing,
# moon brightness
etc = ruleset.etc(45*u.deg, 1.3*u.arcsec, 'dark')
# The target spectrum template.
pickles = SEDTemplate('Pickles_G0V')
# Add the target spectrum from the template with a magnitude
etc.set_target(pickles(18.4*u.ABmag, 'GAIA2r.G'), 'point')
# Get and print the exposure time
texp = etc.get_exptime()
print(f'Exposure time: {texp:.0f}')
Getting the instrument response¶
Another important use case is the retrieval of the instrument response
of the 4MOST instrument under certain conditions. The instrument
response is returned as an astropy.table.QTable with the following columns:
arm : Spectrograph arm (
"blue","green", or"red")wavelength: Wavelength [nm]
binwidth: Spectral bin width [nm]
efficiency: Spectrograph efficiency [electron/photon]
gain: Spectrograph gain [electron/adu]
target: Target signal count [electron]
sky: Sky background count [electron]
dark: CCD dark current [electron]
ron: CCD readout noise [electron]
noise: Noise count [electron]
Note that the table is not sorted by wavelength first, but by the arm, and that in LRS the arms overlap.
As an example, we take the same conditions as before and plot the target and sky spectra and the signal to noise ratio:
import astropy.units as u
import matplotlib.pyplot as plt
from qmostetc import QMostObservatory, SEDTemplate
# Object to simulate the 4MOST observatory, including atmosphere,
# telescope, spectrograph, CCD.
qmost = QMostObservatory('lrs')
# The observation with certain conditions: airmass (zenith angle), seeing,
# moon brightness
obs = qmost(45*u.deg, 1.3*u.arcsec, 'dark')
# The target spectrum template.
pickles = SEDTemplate('Pickles_G0V')
# Add the target spectrum from the template with a magnitude
obs.set_target(pickles(18.4*u.ABmag, 'GAIA2r.G'), 'point')
# Retrieve the result table
res = obs.expose(28*u.min)
# Plot the requested spectra
fig, axes = plt.subplots(2, 1, figsize=(10, 10))
axes[0].set_xlim(560, 800)
axes[0].set_ylim(5, 250)
axes[0].plot(res['wavelength'], res['sky'], color='lightgray')
axes[0].plot(res['wavelength'], res['target'], color='green')
axes[0].set_ylabel(f'Response [{res["target"].unit}]')
axes[1].set_xlim(560, 800)
axes[1].set_ylim(1, 13.5)
axes[1].plot(res['wavelength'], res['target']/res['noise'], color='green')
axes[1].set_xlabel(f'wavelength [{res["wavelength"].unit}]')
axes[1].set_ylabel('SNR per spectral pixel')
plt.show()
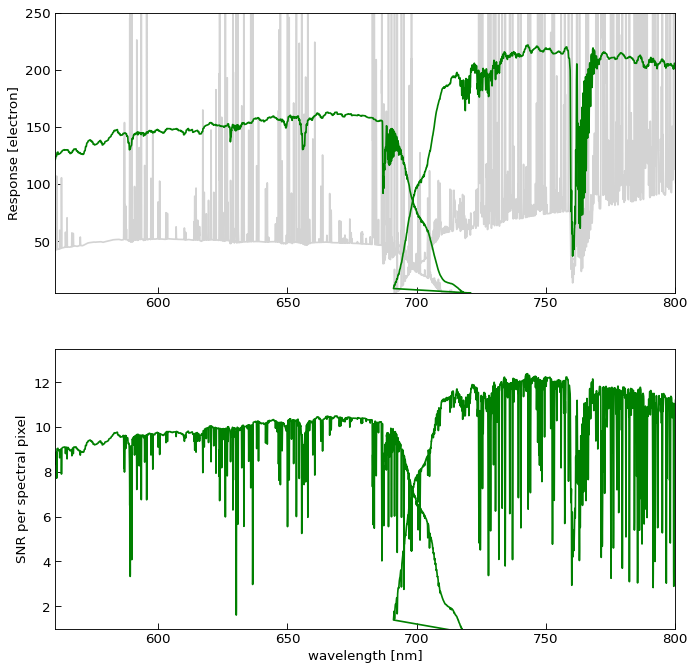
Note that the SNR shown in this simple example is meant per spectral pixel, while in the rule above the SNR was specified per 1 nm. The latter may be calculated by using the binwidth column of the result table.